Um halter é formado por uma barra de massa desprezível e comprimento que sustenta nas suas extremidades duas esferas, cada uma de massa e raio desprezível. Ele está girando em torno de seu centro de massa. Em 3 revoluções, o halter diminui o módulo de sua velocidade angular de e , com aceleração angular cujo módulo é constante.
- Faça um desenho esboçando qualitativamente os vetores angulares inicial, velocidade angular final e aceleração angular.
- Calcule o módulo da aceleração angular do halter.
- Calcule o intervalo de tempo em que ocorre o decréscimo de velocidade descrito.
- Calcule o momento de inercia do halter.
- Qual deve ser o torque aplicado sobre o halter para provocar o decréscimo de velocidade descrito?
Passo 1
a):
Vamos lá:
Só precisamos prestar atenção em:
Primeiro, as duas velocidades angulares, a inicial e final, tem o mesmo sentido, logo os vetores terão o mesmo sentido.
A velocidade final é menor que a inicial, logo, o vetor da aceleração angular tem que ter um sentido contrário ao das velocidades.
Ai fica assim:
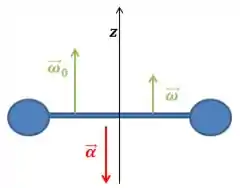
Passo 2
b):
Ai a gente vai usar a equação de Torriceli pro movimento circular:
Mas veja só, quanto vale:
Se foram três revoluções completas:
Então:
Então, o módulo da aceleração é:
Passo 3
c):
Vamos usar a equação:
Então:
Passo 4
d):
O momento de inercia total vai ser a soma dos momentos de inercia de cada bolinha:
Com:
Só que:
Então:
Passo 5
e):
Aqui a gente usa a definição de torque:
E a direção é dada em z, como na figura:
Resposta
a):
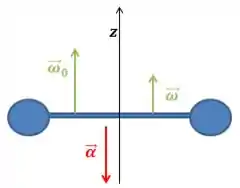
b):
c):
d):
e):