As duas questões abaixo relacionam-se à figura:

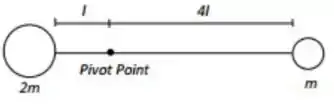
2. Um sistema é formado por dois corpos, um com massa m e o outro com massa 2m, que estão ligados por uma haste rígida sem massa de comprimento 5l. Como mostrado na figura acima, o sistema pode girar ao redor de um eixo horizontal que atravessa o “Pivot Point”. O sistema está sob a ação da aceleração da gravidade g. Quando o sistema é liberado, a haste começa a rodar com uma aceleração angular cuja magnitude é:

a)

b)

c)

d)

e)

3. Em que momento a aceleração angular se anula?

a) Nunca.

b)Quando o sistema se encontra na vertical.

c) Quando o sistema encontra-se na horizontal, com as posições das massas invertidas.

d) No momento que o torque é máximo.

e) Nenhuma das anteriores.

Bom, um dos pesos, o da bolinha de massa , faz a barra girar no sentido horáio, já o outro, no anti-horário. Vamos considerar o sentido anti-horário como positivo dessa vez. Assim:

A outra bolinha exerce um torque negativo:

O torque total será:

Calculando o momento de inercia do conjunto:

Primeiro, precisamos calcular o centro de massa do conjunto. Se coincidir com a posição do pino, tudo bem, mas se não coincidir, vamos ter que usar o teorema dos eixos paralelos.

Assim:

Usando como a posição da bolinha mais pesada:

Ops, como não coincidiu, a gente vai ter que usar o teorema. Mas vamos calcular primeiro

Assim:

Mas quanto vale esse Bom, é a distancia do centro de massa ao pino. Então:

E:

Então:

Assim:

Então o módulo é:

A resposta:

e)

3: A resposta pra isso é simples, vai ser quando o sistema estiver na vertical, pois ai o ângulo entre o braço do torque e a força do torque vai ser 0. Isso acontece já que:

Se