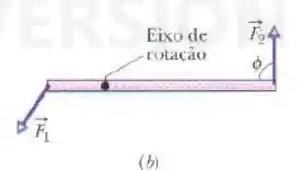
A figura abaixo mostra uma vista superior de uma barra horizontal que gira em torno de um eixo sob a ação de duas forças horizontais, e , com fazendo um ângulo com a barra. Ordene os seguintes valores de de acordo com o módulo da aceleração angular da barra, do maior para o menor: e .
Passo 1
Para analizarmos a variação da aceleração angular com o valor de , precisamos de uma expressão que relacione essas duas variáveis.
Vamos usar a irmãzinha da segunda lei de Newton:
Passo 2
Beleza, temos que encontrar o torque total :
A força tem módulo e direção fixa, além de não ser de nosso interesse nesse problema. Portanto, deixemos o torque realizado por ela como mesmo.
Já na força , apesar de ter o módulo fixo, há uma variação do ângulo que a força faz com o vetor direção. Logo:
Onde é a distância do eixo de rotação para o ponto de aplicação da força, que se mantém fixa.
Passo 3
Juntando as equações:
Temos:
Como queremos analisar a variação da aceleração angular :
Passo 4
Com os ângulos em questão, temos o seguinte:
Logo:
- ''