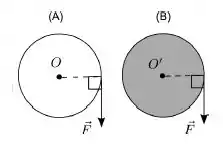
Dois discos A e B de mesmo raio estão sobre uma mesa horizontal e plana e fixados por pinos nos seus centros, em torno dos quais podem girar livremente. Ambos os discos tem sua massa distribuída de maneira uniforme na sua área, mas o disco A tem massa maior que o disco B. Num dado instante começa a atuar sobre ambos, que inicialmente estavam em repouso, uma mesma força na periferia de cada um, como mostra a figura. Para os módulos dos torques resultantes e e das respectivas acelerações angulares e tem-se que:

(a) ;

(b) ;

(c) ;

(d) ;

(e) ;

(f) ;

(g) ;

O torque de uma força é dado pelo produto vetorial entre a posição de aplicação da força e a própria força :

Como esses vetores são perpendiculares, o valor do torque é apenas o produto dos módulos da posição (distância do centro) e da força:

Agora vamos comparar os dois casos. Em ambos tanto a distância do centro quanto a força são iguais. Logo, os torques em A e em B serão iguais:

Vamos à aceleração angular. Podemos relacionar torque com a aceleração angular de cada corpo a partir da expressão:

Então vamos olhar para o momento de inércia de cada um dos discos.

O momento de inércia de um disco é dado por:

Porém, nem precisamos pensar nessa fórmula. Como os dois discos têm a mesma geometria, o disco que apresenta maior massa terá um momento de inércia maior, no caso, será o disco A. Então:

Agora, vamos voltar a pensar na relação entre torque e aceleração angular. Se os dois discos têm um mesmo torque agindo sobre eles, o produto entre e deve ser o mesmo para os dois:

Então, como o momento de inercia de A é maior, sua aceleração angular deve ser menor:

Isso faz sentido, né?

Pois momento de inércia é justamente a resistência que um corpo apresenta de entrar em rotação. Então, para o mesmo torque (“força”), o disco A apresenta uma resistência maior a entrar em rotação e por isso terá uma aceleração angular menor.

Temos então: