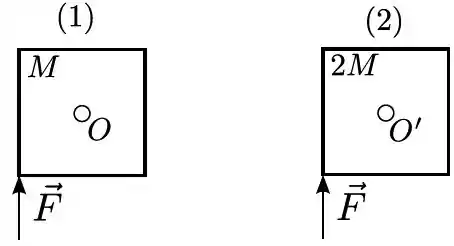
Duas chapas quadradas (1) e (2) de lados iguais têm massas e , respectivamente, e estão presas em uma parede vertical pelos seus centros e , em pinos em torno dos quais podem girar sem atrito. Aplica-se em cada uma delas uma mesma força , vertical de baixo para cima, como mostra a figura. A opção que correlaciona os módulos de seus torques e e suas acelerações angulares e imediatamente após a aplicação de é:
(a)
(b)
(c)
(d)
(e)
Passo 1
O torque de uma força aplicada num ponto com vetor posição em relação a um eixo é, de maneira geral, dado por:
Nessa questão é a mesma força que está atuando nos 2 quadrados, e no mesmo lugar. E os quadrados têm as mesmas dimensões então o vetor posição do ponto de aplicação das forças é o mesmo pros 2!
Logo,
Então é claro que os módulos também são os mesmos:
Passo 2
Show, vamos pra aceleração angular!
O torque resultante se relaciona com a aceleração angular da seguinte maneira (em módulo):
Então pras chapas quadradas 1 e 2, temos, respectivamente:
Vimos que , logo:
Passo 3
Então fica a pergunta: qual chapa tem o maior momento de inércia em relação ao eixo passando pelo seu centro de massa? A chapa de massa ou a chapa de massa ?
É intuitivo pensar que a chapa de maior massa é a que tem maior momento de inércia, mas isso por si só não justifica. Porque se toda a massa de uma chapa estiver concentrada no seu CM, o seu momento de inércia em relação ao eixo que passa pelo CM é nulo, por mais pesada que a chapa seja.
Lembrando que pra calcular o momento de inércia de uma partícula em relação a um eixo, fazemos:
Passo 4
Enfim, no nosso caso não tem problema, porque as chapas são idênticas! Então a de maior massa é a que tem o maior momento de inércia mesmo:
Ou seja, pra equação ser respeitada, devemos ter:
Resposta
Alternativa (a)