Em termos dos vetores unitários, qual é o torque em relação à origem a que está submetida uma partícula localizada nas coordenadas () se esse torque se deve (a) a uma força de componentes e (b) a uma força de componentes ?
Passo 1
A gente aprendeu que torque é um produto vetorial, entre um vetor Força e um vetor Raio (Braço)
Então o que vamos fazer nesse exercício é calcular os torques gerados pela força para a letra e para força para letra .
O enunciado nos diz que em ambos os casos temos um raio , sendo , vetores unitários dos eixos e respectivamente.
Vamos fazer um desenho pra gente visualizar melhor esse braço de alavanca.
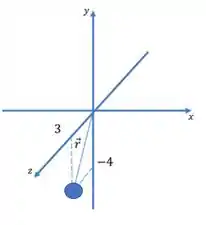
Agora vamos pra cada uma das forças calcular o torque de cada uma das forças agindo na partícula em relação a origem, beleza?
Passo 2
(a) Por ser um exercício em 3 dimensões fica difícil representar a imagem, mas “planificando” nossas dimensões:
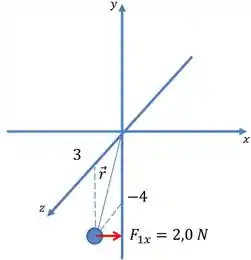
Um detalhe que facilita um pouco a nossa vida é que a força só possui componente em como mostrado no desenho, daí o produto vetorial fica:
Poderíamos resolver de forma matricial ou usando distributiva, nesse caso usaremos a distributiva.
Podemos usar uma regrinha aqui pro sinal do produto vetorial com essa figura aqui:
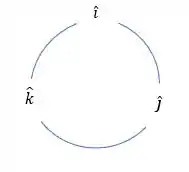
Só pensar no sentido do produto, se o sentido for horário o resultado é positivo e se o sentido for anti horário é negativo. Na primeira parcela temos:
de para o sentido é anti-horário e o resultado dessa parcela é negativo.
de para o sentido é horário e o resultado dessa parcela é positivo.
então:
Passo 3
(b) Realizando a mesma coisa para :
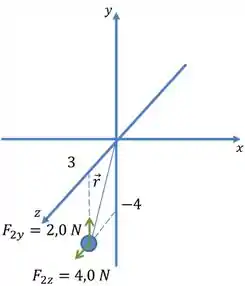
O produto vetorial entre dois vetores que estão no mesmo sentido vale 0 (lembra que na fómula aparece , logo:
Usando aquela regra do sentido, podemos encontrar pra cá também o resultado do produto vetorial.
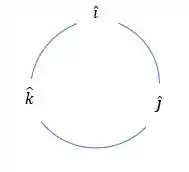
A parcela de para vai dar pra gente , a outra parcela de para vai nos dar algo no sentido , assim temos:
Resposta
a)
b)