Em uma gangorra de parque, uma criança de se senta em uma extremidade da gangorra, enquanto uma criança maior, de g, se senta na outra extremidade. Quando a criança menor tira o pé do chão, calcule a intensidade da força Normal do chão no pé da criança maior. Considere que a gangorra se mantem sempre na horizontal.
- Zero.
Passo 1
Bom galera, essa é uma questão envolvendo basicamente o torque de um sistema. Como a gangorra é um sistema que pode girar, mas queremos que ela esteja sempre na horizontal, a gente precisa fazer com que o torque sobre ela seja nulo.
Podemos fazer um desenho esquemático da coisa toda assim:
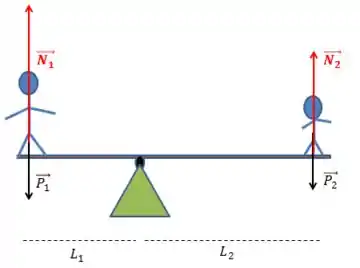
Bom, apesar do meu lindo desenho, vamos imaginar que os bonequinhos estão com o pé no chão inicialmente. Isso gera as normais.
Além disso, veja que a criança maior é da esquerda, e a menor a da direita.
Bom, de inicio, cada normal é igual ao seu peso.
Fazendo o cálculo da soma dos torques é igualando a zero, já que estamos considerando que a gangorra sempre ficará na horizontal:
Consideramos o sentido horário positivo.
Assim:
Assim:
Bom, daqui a gente não tira muitas informações.
Mas, podemos ser espertos, e analisar, por exemplo, só o torque dos pesos:
Passo 2
Beleza, já sabemos a razão entre os braços de alavanca da gangorra. Agora vamos estudar a segunda ocasião: Agora não existe mais uma , já que a criança menor tirou o pé do chão.
Nossa missão é achar a nova
Bom, nesse caso, a soma dos torques vai assumir a forma:
Substituindo:
Então:
Então, nesse caso, a primeira normal também se anula:
e)
Resposta
e)