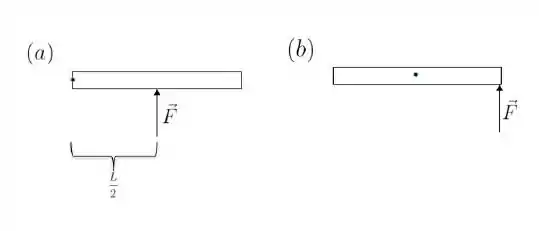
Nas duas situações a seguir, as barras são idênticas, têm comprimento e estão sobre uma mesa de atrito desprezível. Enquanto na situação (a) a barra está presa por uma extremidade, em (b) ela está presa em seu centro. Além da força exercida pelo pino que prende a barra à mesa há uma força externa atuando em cada barra, nas posições indicadas na figura abaixo. Sobre o módulo do torque resultante e o módulo da aceleração angular em relação ao ponto fixo de cada barra, é correto afirmar que:
a) e
b) e
c) e
d) e
e) e
f) e
Passo 1
Sabemos que o torque é dado por:
Onde é a distância da linha de ação da força ao eixo de rotação. Em ambos os casos temos:
Passo 2
Já para encontrar a aceleração angular, vamos usar que:
E então:
No entanto, sabemos que:
E:
Portanto:
Logo:
Resposta
(a)