Energia Potencial e Conservação da Energia Mecânica, Rotação
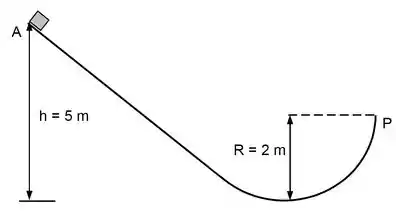
Um bloco de massa desconhecida é solto do repouso na posição em uma rampa sem atrito com formato de quarto de círculo ilustrado abaixo. Calcule a componente radial da aceleração e o módulo da aceleração angular do bloco quando ele atingir a posição P.
Utilize
nenhuma das respostas acima.
Passo 1
Para determinar a componente radial da aceleração, iremos utilizar a Lei da Conservação da Energia Mecânica:
Conservando do ponto até o ponto , temos, considerando a massa do bloco:
Ah...só lembrando que como o bloco sai do repouso, sua energia mecânica em é puramente potencial gravitacional.
Isolando a velocidade, temos:
Substituindo os valores, fica:
Agora podemos determinar a componente radial da aceleração, pois sabemos que .
Passo 2
Agora vamos determinar a velocidade angular do bloco em . Sabendo que em a aceleração tangencial do bloco é a aceleração da gravidade, temos:
Para a aceleração angular, teremos:
Resposta