UFRJ – Física 1 2020.2 – P2 – Questão 8
Calcule o momento angular de um sistema constituído de duas partículas, e , em relação ao ponto , no instante indicado na figura. As massas e as velocidades das partículas e , respectivamente , , e . Considere o eixo positivo para fora da prova.
Escolha uma:
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
O módulo do momento angular é calculado assim:
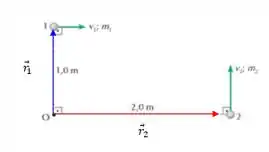
O vetor deslocamento está representado em azul e a vetor em vermelho.
O ângulo entre o vetor velocidade e o deslocamento até o eixo de rotação é para as duas partículas. Agora vamos ver o sinal. Usando a regra da mão direita, vemos que o momento angular produzido pela partícula aponta para dentro da página (portanto negativo) e o momento angular produzido pela partícula aponta para fora da página (portanto positivo).
Então a direção do momento angular vai estar ao longo do eixo . Só nos resta saber o sentido.
Beleza até aqui?
Passo 2
O momento angular total é a soma dos dois momentos. Então temos:
Os dados são:
Assim o vetor momento angular resultante é .
Analisando as alternativas, a correta é a (g).