Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Torque

Ver Teoria
Exercício 961234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495979899100

Enunciado

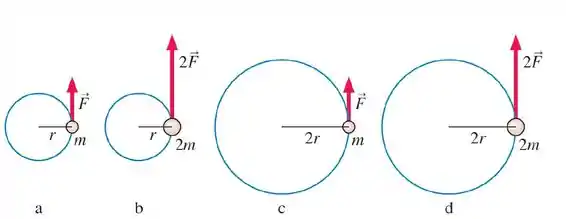
O ordenamento correto das magnitudes das acelerações angulares α a a α d das massas pontuais em trajetórias circulares é:

(a) α a < α b < α c < α d

(b) α d < α c < α b < α a

(c) α a = α b < α c < α d

(d) α c = α d < α a = α b

(e) α a = α c < α b = α d

Passo 1

Beleza, temos trajetórias circulares de raios diferentes e percorridas por corpos com massas diferentes e ainda temos umas forças aplicadas ali na tangente do círculo. A gente quer saber quem tem aceleração angular maior/menor do que o outro.

Quando a gente vê alguma coisa com círculo já fica tentado a usar aquelas equações da cinemática angular, né? Mas o problema é que nesse caso não conhecemos nada sobre a velocidade angular.

E agora?

Vamos voltar lá na figura e ver o que nós temos: r,F...r e F...r e F...opa! r F sen ⁡ θ = τ

Que é a fórmula pra gente calcular o módulo do torque.

E a relação com a aceleração angular é dada por:

τ = I α

Passo 2

Então vamos calcular o torque e usar a relação com a aceleração angular para cada corpo:

Para o corpo a:

τ a = r F sen ⁡ 90 = r F

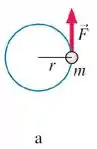
Então

τ a = I α a

α a = τ a I

Lembrando que o momento de inércia de uma massa pontual é:

I = m d 2

Onde d é a distância da massa até o eixo de rotação. O eixo tá passando pelo centro do círculo, saindo da página, confere? Então essa distância é o próprio raio do círculo.

Assim:

I = m r 2

Então:

α a = τ a m r 2

α a = r F m r 2

α a = F m r

Beleza! Guarda esse valor aí. Vamos para o próximo corpo.

Passo 3

Para o corpo b:

τ b = r 2 F sen ⁡ 90 = r 2 F

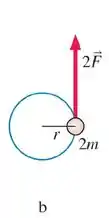
Como

α b = τ b I

o momento de inércia de uma massa pontual é:

I = m d 2

Para o corpo b de massa 2 m e d = r :

I = 2 m r 2

Então:

α b = τ b 2 m r 2

α b = 2 r F 2 m r 2

α b = F m r

Comparando com α a , já vemos que:

α a = α b

Vamos para o próximo corpo.

Passo 4

Para o corpo c:

τ c = 2 r F sen ⁡ 90 = 2 r F

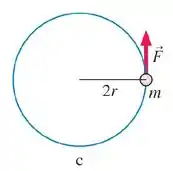
Como

α c = τ c I

o momento de inércia de uma massa pontual é:

I = m d 2

Para o corpo c de massa m e d = 2 r :

I = m ( 2 r ) 2

I = m 4 r 2

Então:

α c = τ c 4 m r 2

α c = 2 r F 4 m r 2

α c = F 2 m r

Opa! Comparando com α a = α b , já vemos que:

α c < α a = α b

Vamos para o próximo corpo.

Passo 5

Para o corpo d:

τ d = 2 r 2 F sen ⁡ 90 = 2 r 2 F = 4 r F

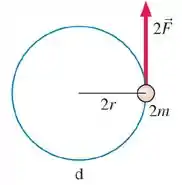
Como

α d = τ d I

o momento de inércia de uma massa pontual é:

I = m d 2

Para o corpo d de massa 2 m e d = 2 r :

I = 2 m ( 2 r ) 2

I = 8 m r 2

Então:

α d = τ d 8 m r 2

α d = 4 r F 8 m r 2

α d = F 2 m r

Show! Então comparando tudo:

α d = α c < α a = α b

Resposta

Alternativa D

Exercícios de Livros Relacionados

Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2