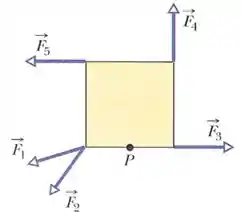
As cinco forças mostradas na figura, todas de mesmo módulo, agem sobre uma placa quadrada que pode girar em torno do ponto . Ordene as forças em ordem crescente do módulo do torque que cada uma exerce em relação ao ponto .
(A)
(B)
(C)
(D)
(E)
Passo 1
Temos que o torque é dado por
E seu módulo é dado por
Onde é o ângulo entre os vetores e .
Quando , temos então que o torque é nulo. E é isso que acontece para a força , o vetor ligando o ponto até o ponto onde a força age é paralelo a .
Temos que quando , o torque é dado pelo produto . Assim quanto mais perto de maior será o torque. Vendo isso podemos comparar os torques das forças e . Como a força está mais perto de ser perpendicular do que a força temos que
Agora as forças e agem em pontos que estão a uma distância maior que o dobro das distâncias que as forças e agem, assim essas forças têm um braço de força maior.
Agora comparando essas duas vemos que a força faz um ângulo mais próximo de do que a força , assim
De forma que
Resposta
(D)