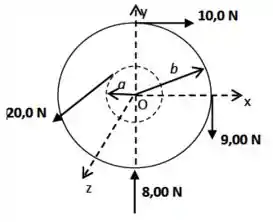
Sobre o disco de raio , situado no plano , são aplicadas as forças como mostra a figura. As forças de e tangenciam o disco, a força de é normal do disco e a força de tangencia o círculo de raio . Qual o torque resultante sobre o disco, em relação ao eixo que passa por e perpendicular ao disco. Considere e .

Para determinar o torque resultante, vamos relembrar sua definição:

Vamos calcular o torque gerado por cada força separadamente e depois somamos tudo para determinar o torque resultante!

Para a força de , como temos que o vetor e o vetor são perpendiculares, temos:

Repare que a direção do vetor torque é dada pela regra da mão direita!

Para a força de , como temos que o vetor e o vetor são perpendiculares, temos:

Para a força de , como temos que o vetor e o vetor são perpendiculares, temos:

Não esqueça da regra da mão direita!

Para a força de , temos que o vetor e o vetor são paralelos, portanto, o torque é nulo!

Agora que temos todos os torques, basta somar e calcular o torque resultante: