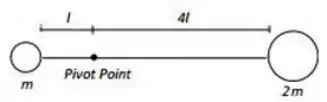
Um sistema é formado por dois corpos, um com massa e o outro com massa , que estão ligados por uma haste rígida sem massa de comprimento . Como mostrado na figura, o sistema pode girar ao redor de um eixo horizontal que atravessa o “Pivot Point”. O sistema está sob a ação da aceleração da gravidade . Quando o sistema é liberado, a haste começa a rodar com uma aceleração angular cuja magnitude é:

a)

b)

c)

d)

e)

Podemos calcular a aceleração angular pela fórmula:

Para isso precisamos achar o torque resultante e o momento de inércia desse sistema.

Torque resultante:

Substituindo para o problema aqui, onde a força é o peso dos corpos e é a distância ao eixo de rotação.

Agora só falta calcular o momento de inércia que é calculado pela fórmula:

Substituindo os dados do problema:

Agora substituindo na fórmula da aceleração angular: