Uma barra delgada homogênea de massa e comprimento encontra-se suspensa horizontalmente com a extremidade apoiada na borda de uma mesa e a outra extremidade suspensa por um fio inextensível e de massa desprezível preso ao teto. O fio é cortado com uma tesoura e o instante imediatamente após o corte será chamado de .
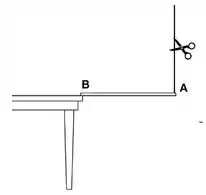
(a) Adote um sistema de coordenadas, esboce o diagramas de forças sobre a barra antes e imediatamente após o corte do fio. Escreva todas as forças explicitamente nas duas situações acima em termos da base de versores adotada.
(b) Antes do corte do fio, ou seja, para , determine a magnitude das forças e .
(c) Determine o vetor torque com respeito ao ponto no instante .
(d) Determine o vetor aceleração angular da barra em ao girar em torno de um eixo passando por .
(e) Determine o vetor aceleração do centro de massa em .
(f) Determine a força de reação da mesa sobre a extremidade da barra em . Qual a razão entre a magnitude dessa força em e em ?
IMPORTANTE: Deixe todas as suas respostas em termos apenas das variáveis fornecidas no enunciado, da aceleração gravitacional local () e dos versores da base adotada.
Passo 1
Opa!! Vamos lá! Temos uma barra presa com um fio e apoiada na mesa. Aí em um certo momento eles cortam o fio, aí aquela ponta da barra que tava sendo presa pelo fio cai. Nisso que ela cai ela descreve um pedaço de trajetória circular. Beleza?
Então vamos lá.
Passo 2
(a)
Ele quer dois diagramas de forças, um quando o fio tá lá e outro depois que cortaram o fio.
A barra tem massa então sofre a atração gravitacional, logo temos o peso, em ambas situações.
Quando temos fio, existe tensão no fio.
Além disso, a barra tá apoiada na mesa,que é uma superfície, então temos uma normal em ambos os casos.
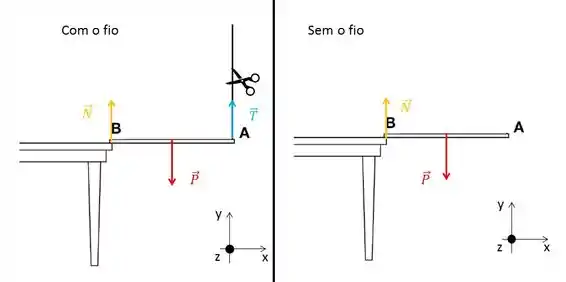
Coloquei ali embaixo os nosso eixo de coordenadas, onde x e y estão no plano e z sai da página.
Agora vamos escrever as forças explicitamente, como ele pede:
Com o fio:
Sem fio:
Show! Vamos para o próximo.
Passo 3
(b)
Só uma observação, as forças no ponto A,, e no ponto B, , são respectivamente a tração e a normal. Só olhar na figura anterior. Beleza?
Então, quando ainda temos o fio, a barra está parada, ela está em equilíbrio!
As condições de equilíbrio são:
Usando a primeira condição:
Na letra (a) escrevemos essas forças explicitamente, então vamos usar elas:
Beleza..guarda essa aí.
Vamos ver a outra condição de equilíbrio agora:
Como o normal tá aplicada em cima do eixo de rotação, então ela não produz torque, beleza? O peso e a tração produzem em relação ao eixo que passa pelo ponto B.
Vamos calcular o torque de cada um deles:
Lembrando que o é a distância do eixo de rotação até o ponto em que a força tá sendo aplicada. Como o peso tá aplicado no CM da barra, que é o meio da barra, temos que:
Então:
Agora, vamos calcular o torque da tração:
Agora o porque a tração tá aplicada lá no final da barra.
Show! Agora vamos voltar pra nossa condição:
Arrumando isso:
Uhul! Essa é a força que ele pediu pra gente!
Pra gente achar a , ou seja a normal, vamos lembrar da condição de equilíbrio para as forças que a gente fez lá em cima:
Já sabemos o e o , então é só substituir:
Maravilha!
Passo 4
(c)
Agora ele pede pra gente achar o torque em relação ao ponto B quando cortamos o fio.
Nessa situação, só temos o peso e a normal atuando. Mas a normal tá em cima do eixo, que passa pelo ponto B, então o torque dela é nulo (porque ).
Logo, só vamos ter o torque do peso. Que calculamos ali em cima:
Passo 5
(d)
Agora ele quer a aceleração angular que a barra tem quando o fio é cortado.
Para isso, vamos usar a relação do torque com a aceleração angular:
Vimos na letra (c) que só temos o torque do peso, então já sabemos o valor dele.
Temos que descobrir o momento de inércia agora.
O valor tabelado para o momento de inércia de uma barra que gira em torno de um eixo que passa pelo centro de massa é:
Mas nesse nosso problema o eixo de rotação tá passando pelo CM?
Não né! O eixo tá lá na extremidade da barra.
Então, pra gente descobrir o momento de inércia em relação a esse eixo da extremidade, vamos usar o teorema dos eixos paralelos:
Lembrando que o é a distância do CM até o nosso eixo novo, e que no nosso caso vale , olha aí na figura pra você lembrar:
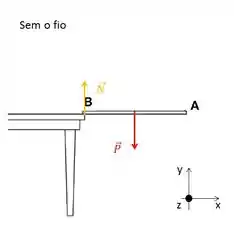
Então:
Resolvendo essa continha:
Maravilha! Já podemos descobrir a aceleração angular
Ajeitando isso daí:
Passo 6
(e)
Agora na letra (e) ele pede a aceleração do CM, que é dada por:
Lembrando que:
A gente não sabe o valor do , mas sabemos sua direção e sentido, pela regra da mão direta, se a gente girar os dedos no mesmo sentido de rotação da barra, o nosso dedão vai estar apontando pra dentro da folha, certo?
E o é o raio da trajetória circular, em relação ao CM:
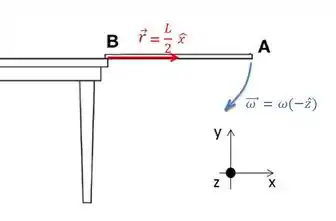
Então:
Como falamos antes:
E quem é ? (Só o módulo, ok?
Então:
Show!
Passo 7
(f)
Vamos olhar de novo pro nosso diagrama quando o fio é cortado:
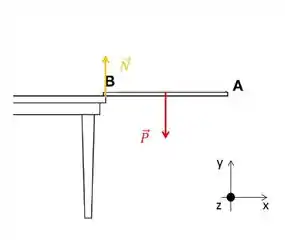
A força em B é a normal, certo?! Então, aplicando a segunda lei:
Acabamos de achar a na letra (e):
Ajeitando isso:
Como ela aponta para cima:
Beleza! Essa é a nossa força em B depois que cortaram o fio.
Agora a gente precisa achar a força em B (normal) quando o fio ainda estava lá e calcular a razão de uma pela outra!
Quando o fio ainda tava lá:
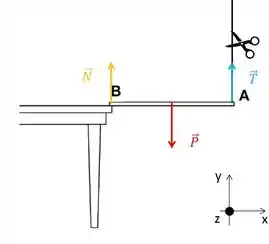
Pela segunda lei:
A gente achou a tração lá na letra (b), e como o conjunto tava parado, a aceleração é zero.
Como ela tá apontando pra cima:
Finalmente, vamos calcular a razão da força em B(normal) antes de cortarem o fio e depois de cortarem o fio:
Resposta
(a)
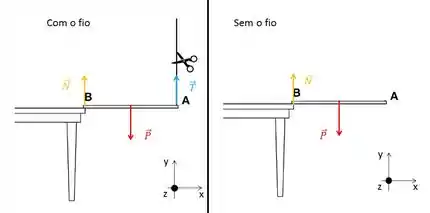
Com o fio:
Sem fio:
(b)
(c)
(d)
(e)
(f)
Sem o fio:
Com o fio:
Razão entre elas: