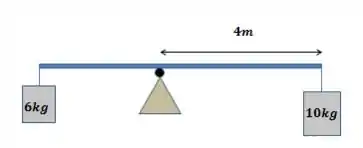
Dois corpos de massa e estão sujeitos à ação da gravidade e são pendurados por cordas naextremidade de uma barra de massa desprezível. A barra é apoiada sobre um ponto distante de uma de suas extremidades e permanece em equilíbrio, como mostrado na figura abaixo. Se a corda de apoio ao bloco é cortada encontre o torque agindo no sistema em relação ao ponto de apoio da barra.
Obs: Alteramos as opções, já que a questão foi anulada.
Passo 1
Bom, o corpo encontra-se em equilíbrio.
O que isso quer dizer? Quer dizer que o somatório dos torques em relação ao ponto de apoio é zero.
Passo 2
Vamos considerar que o sentido anti-horário é o positivo. Então, o torque 1, causado pela massa de , é positivo, e o torque causado pela massa de , negativo.
Já é?
E o torque final é nulo, então:
Então:
Passo 3
E o que isso quer dizer? Quer dizer que a gente não precisa saber a distância de aplicação da força peso dos pra calcular o seu torque. Conseguimos apenas sabendo que o sistema estava em equilíbrio (:.
E o que acontece se a a corda que segura o corpo de for cortada? Bem, nesse caso, o torque 2 some, e o torque resultante passa a ser o próprio torque 1:
Então:
a)
Resposta
a)