UNB, UnB - Gama, Física 1, P3 - 2017.2, Questão 3.
3. Em um motor elétrico típico, a curva de torque é aproximadamente constante na faixa de rotações de trabalho do motor. Suponha que o eixo deste motor está conectado à uma roda de massa , em formato de cilindro. Sabendo que o torque do motor é dado por , obtenha a aceleração angular e a velocidade angular em função do tempo .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
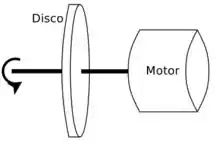
Nesse problema queremos obter a aceleração angular e a expressão que descreve a velocidade angular com o tempo de um disco cujo centro de massa está ligado a um motor que produz um torque constante .
Tem alguma ideia do que podemos fazer? 🤔
A expressão que relaciona o torque à aceleração angular é dada por
E com obtido, substituímos na expressão .
Sacou? Bora começar! 😉
Passo 2
Da equação , sabemos que é uma constante que vamos chamar de e é o momento de inercia do disco dado por
Substituindo essas informações na equação, temos
E por fim, substituindo em , temos
A velocidade angular inicial é , então
É isso! Essa resolução te ajudou? Responde Aí! ✌
