Uma pequena esfera de massa está presa a um fio ideal de comprimento , que tem a outra extremidade presa a um ponto no teto. A esfera está presa a uma mola ideal que se encontra na horizontal e tem sua outra extremidade presa na parede. No instante mostrado na figura, a mola se encontra comprimida em relação a seu comprimento natural e exerce sobre a esfera uma força de módulo .
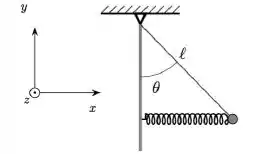
No sistema de eixos indicado na figura, qual o torque que a força elástica da mola exerce sobre a esfera em relação ao eixo paralelo a , que passa pelo ponto de sustentação do fio?
a) O torque é nulo
b)
c)
d)
e)
f)
g)
Passo 1
Se lembra do que a gente usa pra calcular o torque, certo ?
Sendo a força perpendicular à distancia
No nossa questão nós sabemos que essa distância é o tamanho da corda, ou seja:
A força que está sendo exercida no pendulo é a , porém ela não é perpendicular à corda, ou seja, precisamos usar somente a componente perpendicular.
Se a gente lembrar um pouquinho de trigonometria, a gente consegue melhorar essa fórmula pra colocar nas opções
Sendo assim, como ainda estamos trabalhando com relação ao eixo , precisamos colocar o vetor.