Um quadrado homogêneo de madeira de comprimento de lado é colocado sobre uma mesa horizontal e está livre para girar em torno de seu eixo central. O quadrado está sujeito a duas forças como mostrado na figura. Qual a magnitude do torque resultante sobre o quadrado em relação ao eixo de rotação?
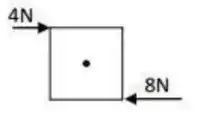
(Obs.: Alteramos as opções, já que esta questão foi anulada.).
Passo 1
Bom galera, essa questão foi anulada, mas vamos resolver mesmo assim.
Ela é bem simples, só a gente calcular o torque de cada força e depois soma-los, pra achar o torque resultante.
Passo 2
Bom, a grande complicação aqui é saber a distância do braço do torque.
Bem, como isso é uma quadrado, e as forças agem paralelamente aso lados, os braços do torque serão a metade dos lados.
Assim:
E:
Passo 3
Então, o torque resultante será:
Por que somamos? Veja, as forças fazem o quadrado girar no mesmo sentido, ou seja, o sentido horário.
Então:
d)
Resposta
d)