Considere um haltere formado por duas pequenas esferas de massa , presas por uma barra de comprimento e massa desprezível. O sistema repousa em uma mesa horizontal sem atrito quando começam a atuar, simultaneamente, duas forças e de mesmo módulo conhecido . A força atua em uma das esferas, na direção da barra e a força atua na outra esfera, em uma direção perpendicular a , conforme mostra a figura.
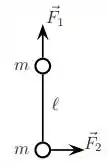
Pode-se afirmar que no instante em que as forças começam a atuar:
(a) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(b) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(c) O módulo do torque resultante em relação à posição do centro de massa da barra é .
(d) A aceleração angular do haltere em torno do centro de massa se relaciona com a aceleração do centro de massa por .
(e) A aceleração angular do haltere em torno do centro de massa se relaciona com a aceleração do centro de massa por .
(f) A aceleração do centro de massa é nula.
(g) A aceleração angular em torno da posição do centro de massa do sistema é nula.
Passo 1
Temos duas forças e aplicadas nesse sistema.
As alternativas falam sobre o torque resultante em relação ao centro de massa, sobre a aceleração do centro de massa e sobre a aceleração angular
Então vamos calcular cada um desses caras.
Passo 2
Vamos começar com a aceleração do centro de massa .
Podemos encontrar a aceleração do centro de massa simplesmente aplicando a segunda lei de Newton:
A massa do sistema será apenas a soma das massas das bolinhas, pois a haste tem massa desprezível:
Já a força resultante será a soma dos vetores e .
Como e são perpendiculares, o módulo da força resultante será:
Ambas as forças têm módulo :
Assim, temos que a aceleração do centro de massa é:
Passo 3
Agora vamos achar torque com relação ao centro de massa.
Para isso, primeiro vamos achar a posição do centro de massa.
Como as duas partículas têm a mesma massa, o centro de massa estará exatamente no meio delas, ou seja, na metade da haste:
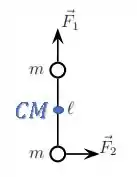
Passo 4
Agora, vamos ao torque...
Uma vez que tivermos o torque resultante, podemos encontrar a aceleração angula , a partir de:
O torque resultante desse sistema é a soma dos torques gerados por cada uma das forças:
O torque da força é dado pelo produto vetorial:
Sendo o vetor , a distância do centro de massa ao ponto de aplicação da força:
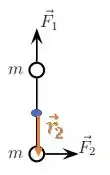
O módulo de será dado pelo produto dos vetores vezes o seno do ângulo entre eles:
Como o ângulo entre eles é (vetores perpendiculares), temos:
A distância será metade do comprimento da haste:
Vamos ao torque de :
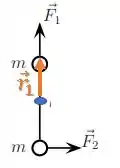
O módulo do torque será:
Nesse caso, os vetores estão na mesma direção :
Logo, a força não gera torque.
Assim, o torque resultante será:
Passo 5
Agora que temos o torque resultante, podemos calcular a aceleração angular com:
Quem é o momento de inércia do sistema?
Como a haste tem massa desprezível, as partículas são as únicas que entram no cálculo de momento de inércia:
O momento de inércia de uma partícula é dado pela sua massa vezes sua distância ao eixo de rotação ao quadrado:
Assim, como as duas partículas têm a mesma massa e a mesma distância ao centro de massa, temos:
Assim, voltanto à nossa expressão de torque, temos:
Passo 6
Vamos aos nossos resultados...
O torque resultante é:
Enquanto a relação entre e podemos construir simplesmente dividindo um pelo outro:
Assim, vemos que apenas a alternativa (a) está correta.
Resposta
Letra (a)