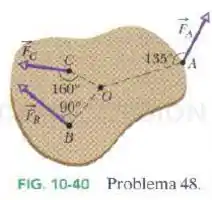
O corpo da Fig. 10-40 tem um eixo que passa por e é perpendicular ao papel. Três forças agem sobre ele: no ponto , a de ; em , a de ; e em , a de . Qual é o torque resultante em relação a ?
Passo 1
Para encontrarmos o torque resultante, iremos realizar a soma vetorial dos torques gerados por cada força.
No entanto, é SUPER IMPORTANTE que você se atente aos sinais de cada torque. Por isso, vamos calcular as intensidades do torque através da fórmula do módulo do torque, mas usaremos a regra da mão direita para definir para que sentido cada um deles aponta.
Definimos o eixo apontando para você como o sentido positivo, e então:
Passo 2
Para calcular o módulo do torque usamos a fórmula:
Lembrando que é o ângulo entre os vetores e . Aplicando a fómula para os pontos A, B e C:
Passo 3
Agora precisamos realizar a regra da mão direita, para descobrir para que sentido apontam os vetores.
Se você reparar na figura, é possível visualizar que, tanto quanto tendem a girar nosso objeto no sentido anti-horário em relação ao eixo de rotação e isso vai gerar um torque que aponta para você, portanto positivo. Já faz o nosso objeto girar no sentido horário, o que gera um torque negativo, já que o dedão aponta no sentido de furar a tela. Logo:
Passo 4
Obtendo o torque resultante: