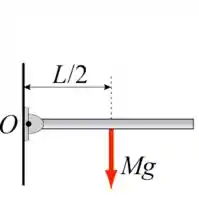
Uma haste uniforme de comprimento e massa pode rodar livremente em torno de um pino passando por uma das extremidades (ponto O). A haste é abandonada na posição horizontal a partir do repouso.

1. Qual é a sua velocidade angular quando ela atinge a posição vertical?
2. Determine a velocidade linear do centro de massa e a da extremidade da haste quando ela está na posição vertical.
3. Qual é o torque na haste e sua aceleração angular em função do ângulo que a haste forma com a posição vertical ?
4. O momento angular da haste em relação ao ponto O se conserva? Justifique sua resposta.

Dado: O momento de inércia de uma haste de massa M e comprimento d em relação a um eixo que passa pelo seu centro de massa é

b):

Pra determinar a velocidade linear do centro de massa, é só a gente aplicar de novo:

Com:

Então:

Agora, pra achar a velocidade da ponta é só fazer a mesma coisa só que mudando o valor do raio:

c):

Bom, o torque será ma´ximo quando o torque da força peso for.

E ele é máximo na horizontal, né? Já que ali o ângulo que o vetor peso faz com o comprimento da barra é de noventa graus.

Esse também é o ângulo que a barra faz com a vertical. Vamos chama-lo de:

Além disso, quando a barra está toda vertical, “em pé”, o torque é nulo, já que o peso fica paralelo ao comprimento da barra.

Assim, nesse momento a barra faz um ângulo zero com a vertical e o torque se anula. Então a função que melhor descreve esse torque oscilante será:

Já que:

Show? Isso tudo ai foi calculado em módulo.

Vamos calcular esse

Porque estamos considerando um torque que age diretamente no centro de massa.

Assim:

Beleza. E a aceleração? Bom, é só usar:

Com:

Assim:

d):

Não se conserva pois o torque externo não é nulo em todo o instante.

Assim:

A não ser quando

Então, o momento angular só se conserva quando a barra fica na vertical.