Um anel de raio tem massa distribuída uniformemente. Ele é posicionado no plano horizontal, de modo que o eixo seja vertical e apontando pra cima, e atravesse o seu centro de massa. O anel gira com aceleração angular . No instante , ele apresenta velocidade angular
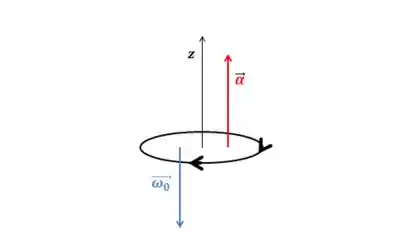
- Faça um desenho mostrando os vetores velocidade angular no instante e a aceleração angular do anel, viso de cima, em Indique se o disco gira no sentido horário ou anti-horário.
- Em que instante o anel terá girado uma revolução completa?
- Em que instante o anel para momentaneamente?
- Calcule o momento de inércia do anel em relação ao eixo
- Qual deve ser o torque(módulo, direção e sentido) aplicado ao anel necessário para o movimento descrito?
Passo 1
a):
Bom galera, o que determina o sentido de rotação desses vetores são os seus sinais no eixo . Depois que a gente sabe ora onde eles apontam, a gente usa a regra da mão direita pra descobrir o sentido de rotação:
Passo 2
Sabemos que uma revolução completa é igual a . Utilizando a equação de Torricelli para descobrir a velocidade angular ao terminar a revolução completa:
Aplicando agora a seguinte fórmula:
Logo,
Passo 3
c):
O que acontece com a velocidade angular quando o anel para momentaneamente?
Ela torna-se zero, não é mesmo?
Então podemos usar a função da velocidade:
Então, nesse tempo
Passo 4
d):
Aqui a gente vai ter que usar definição de momento de inércia a partir da integral:
Show? Beleza, mas como resolver esse integral maluca ae?
Bem, como é um anel, o raio é sempre o mesmo. Assim, é uma constante e sai da integral:
Passo 5
e):
Beleza, ele tá pedindo o torque externo. Mas como você já sabe a aceleração angular do anel e o momento de inércia, fica muito fácil pois é só usar a equação:
Resposta
a):
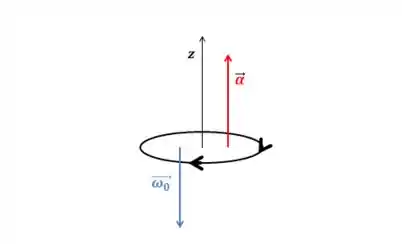
b):
c):
d):
e):