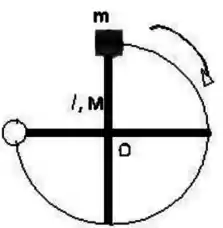
A figura mostra uma haste rígida de massa M e comprimento l, a qual pode girar em torno de um eixo horizontal que passa pelo seu centro de massa (mostrado como ponto O na figura). Há uma força de atrito entre o eixo de rotação e a haste. Uma bolinha de massa m e raio desprezível é conectada a uma extremidade da haste. Inicialmente o sistema está na posição vertical conforme mostra a figura; ele começa a rodar no sentido horário sob efeito da gravidade, até parar numa posição na qual o ângulo de rotação com relação à direção original é de .
- Calcule o trabalho da força de atrito durante o movimento.
- Supondo constante o módulo do torque da força de atrito durante o movimento, qual o seu valor?
- Qual a aceleração angular (módulo, direção e sentido) do sistema em função do ângulo que a haste faz com a horizontal.
Dados:
Para a barra:
Passo 1
a):
Como a força de atrito é uma força dissipativa, podemos dizer que o trabalho dela vai ser igual a variação da energia mecânica. Assim:
A energia mecânica inicial é:
E a final é:
Assim:
Então:
Passo 2
b):
O módulo do torque da força de atrito é dado por:
Mas a gente não sabe o valor disso. Bom, mas sabemos o valor do trabalho da força de atrito.
Se tentarmos calcular o trabalho da força de atrito pela definição simples, vamos chegar a uma coisa legal:
Mas como os dois vetores da equação são paralelos:
E como isso é uma rotação podemos mudar pras coordenadas polares:
Assim:
Show?
Mas quanto vale aquela variação angular ali? Ah, o enunciado já deu:
Assim:
Substituindo o valor do trabalho:
O torque é negativo por que atrasa a rotação do negocio.
Passo 3
Bom, primeiramente, a aceleração angular vai depender do ângulo porque o torque da força peso vai depender dele. O torque da força de atrito é constante, mas o da força peso não.
Depois da gente calcular o torque da força peso, vamos usar a equação:
E descobrir
Bom, naturalmente, a gente nota que quando a barra estiver fazendo com a horizontal, o torque do peso vai ser nulo porque a direção do peso vai coincidir com a barra.
Já quando a bolinha estiver toda deitada, o torque vai ser máximo. Então é de esperar que o torque seja assim:
E ele é sempre positivo porque ele aumenta a rotação do negocio.
Então, o torque total ou resultante é dado por:
Show?
Agora é substituir o valor de
Resposta
a):
b):
c):