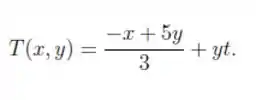Seja o espaço dos polinômios de grau Sejam base de e base de , e seja uma transformação linear cuja matriz é dada por:
Calcular a transformação linear T(x,y).
Passo 1
A questão deu pra gente:

E por fim uma matriz T que transforma vetores de na base em polinômios de na base a partir de:
Passo 2
Vamos ver primeiro como escrevemos um vetor qualquer (x,y) do na base
Queremos encontrar as coordenadas a e b tais que:
Ficamos com o sistema:
Somando as duas equações:
Logo:
Substituindo em qualquer uma das equações, achamos o valor de b:
Passo 3
Agora podemos aplicar a matriz T ao vetor (x,y) na base e achar a transformação do vetor no polinômio de grau menor ou igual a 1.
Fazendo isso:
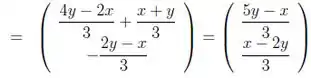
Agora, para escrever esse polinômio na base , fazemos:
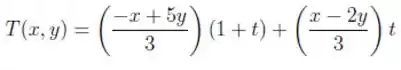
Arrumando os termos:
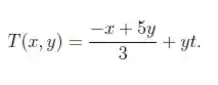
Resposta