Seja a transformação linear que realiza uma reflexão em relação ao plano seguida de uma rotação de ângulo no sentido anti-horário em torno do eixo
a) Determine a matriz canônica de
Passo 1
Faaaala pessoal, bora lá matar mais uma questãozinha de álgebra linear
Antes de tudo, só pra deixar a notação mais fácil: esse exercício considera os eixos . Vamos considerar o basicão ok??
Aqui temos uma transformação linear que faz o seguinte:
- Ela pega o vetor de entrada
- Aí ela reflete esse vetor em relação ao plano
- Por fim, ela roda esse vetor em em torno do eixo no sentido anti-horário

E aí queremos encontrar a matriz canônica dessa transformação linear que faz tudo isso aí hahahaha vamos lá!
Passo 2
Então vamos traduzir cada passo:
- Temos
- A reflexão no plano quer dizer que estamos invertendo o sinal da coordenada
- Quando rodamos o vetor em torno do eixo no sentido anti-horário, estamos fazendo isso aqui:
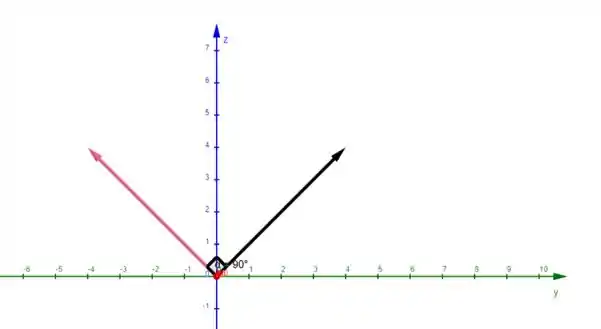
O vetor preto é antes de rodar e o vetor rosa é após a rotação, ok? Repara que a gente manteve a coordenada e invertemos o sinal da coordenada , e o fica igual porque estamos girando em torno dele
Agora se girarmos o vetor rosa vamos obter esse vetor roxo:
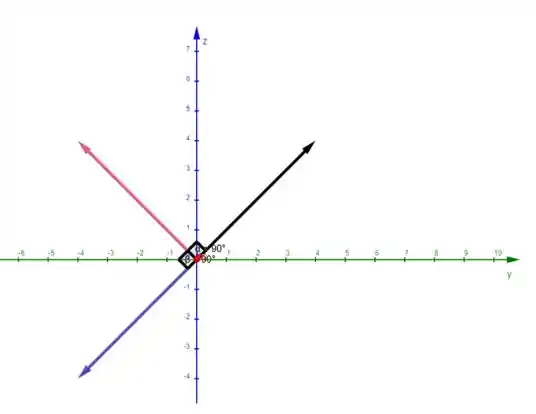
Repara que agora mantivemos a coordenada e invertemos o sinal da coordenada
Ou seja, o que acontece nessa rotação em é o seguinte:
Passo 3
O exercício também pergunta se essa transformação linear pode ser sobrejetora
Sabemos que em uma transformação , se a dimensão de e de forem iguais (como é o nosso caso, já que estamos indo de para ), a transformação vai ser sobrejetora se, e somente se, ela for injetora

Até aqui beleza.
Para que seja injetora, o núcleo dela tem que ter apenas o vetor nulo . Resumindo, o único vetor tal que tem que ser apenas
Opa! Mas a gente acabou de ver no passo 2 que
Ou seja, a transformação não é injetora!!
E PORTANTO, também não é sobrejetora!!
E é isso hahaaha
Resposta
Não pode ser sobrejetora