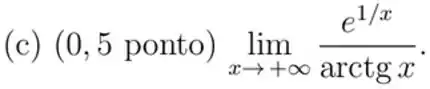
Passo 1
Substituindo:
Aí, repara o seguinte: o arco cuja tangente vale é o ângulo de , ou seja, . Com isso, basta que a gente substitua esse valor e mate o limite:
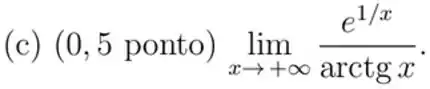
Substituindo:
Aí, repara o seguinte: o arco cuja tangente vale é o ângulo de , ou seja, . Com isso, basta que a gente substitua esse valor e mate o limite: