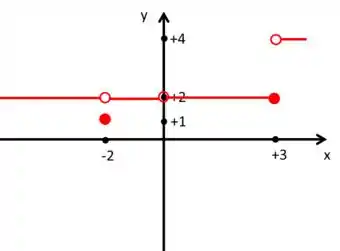
2. Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas.
b.
não está definido.
Passo 1
Oi, galerinha! Tudo bom? Nessa questão podemos esboçar um gráfico qualquer desde que ele atenda a essas seis condições:
O limite de pela direita tem ir para .
O limite de pela direita tem que ir para .
O limite de vai para .
A função no ponto tem que ser igual a .
A função no ponto tem que ser igual a .
E o ponto não está definido.
Bora lá!
Passo 2
Podemos montar um gráfico assim, por exemplo:
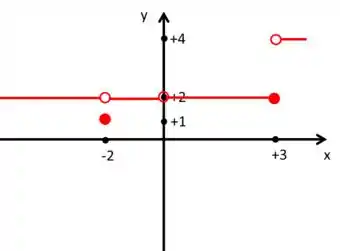
O importante é que a linha que vem pela esquerda e direita para o ponto pare no ponto , pois é para o onde o limite vai e ali tenha uma bolinha vazia (mostrando que ). Aí no caso, vamos colocar uma bolinha preenchida no ponto , pois .
Continunado a linha em direção a direita, temos que colocar uma bolinha vazia em , pois a função não está definida neste ponto. Seguindo a linha, vamos parar com uma bolinha preenchida em , pois o limite de pela esquerda é e .
Já a linha que vem pela direita, deve parar no ponto , onde vamos colocar uma bolinha vazia (mostrando que a função naquele ponto não tem aquele valor).
De resto, podemos fazer qualquer caminho que leve a esses pontos!
Resposta