Considere a função , dada por , e os números , . Para cada intervalo aberto abaixo, encontre um intervalo aberto , centrado em , com a seguinte propriedade:
Passo 1
Opaa!! Seguinte, primeiramente vamos dar uma olhadinha no gráfico da função dada pela questão:
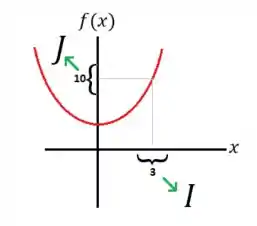
Assim, desejamos descobrir qual o intervalo de valores de pertencentes a centrados em que farão com que esteja sempre contido no intervalo , centrado em .
Passo 2
Dessa forma, vamos substituir os valores dos limites de em para determinarmos os limites do intervalo em .
Assim, o nosso intervalo de é . Ou seja, para :
E, para :
Logo, temos o intervalo .
Legal essa né? Vamo que vamo!!
