Considere a função , dada por:
b) O que podemos afirmar sobre . Justifique sua resposta.
Passo 1
Falaeee, beleza??? Seguinte, vamos relembrar o gráfico que encontramos:
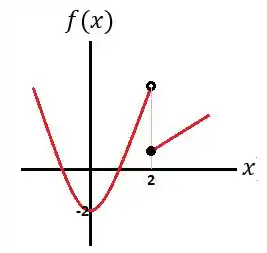
Passo 2
Perceba que:
E que:
Assim, como os limites laterais são diferentes, então
Massa né? Responde Aí!! ;)
