Considere a função f cujo gráfico está representado abaixo. Determine o que se pede.
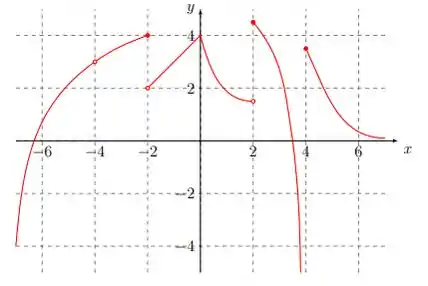
(a) O domínio de .
(b) e o limite
(c) e o limite
(d) e o limite
(e) e o limite
(f ) e o limite
(g) O que se pode dizer sobre a existência do limite nos pontos ?
Passo 1
Oi galera, beleza? Vamos resolver juntos?

Letra (a):
O domínio de uma função são os valores de nos quais ela está definida. Pode tender ao infinito, mas ela existe!
Se você analisar essa função, ela tem alguns valores de nos quais a função tende a menos infinito. Mas não quer dizer que ali ela não esteja definida.
O único ponto que está em aberto e que nesse ponto a função não tem uma definição é em .
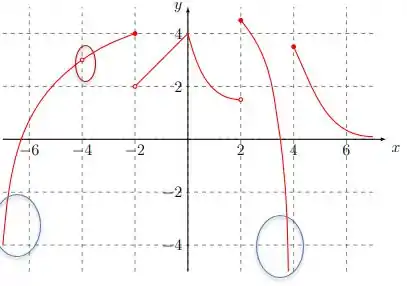
Sendo assim, o domínio de é:
Passo 2
Letra (b):
O limite de uma função é encontrado através dos limites laterais. Se a função tender para o mesmo valor tanto pela direita, quanto pela esquerda, então o limite existe e é o valor dos limites laterais (que vão ser iguais).
Já se os limites laterais forem diferentes significa que o limite da função naquele ponto não existe. Mas mesmo assim a função no ponto pode existir. É o valor onde a curva da com a “bolinha cheia” no gráfico.
Beleza?
Agora vamos aplicar isso aos diversos pontos do problema!
Primeiro em . Dá uma olhada no gráfico:
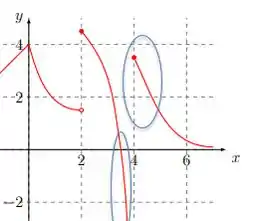
Quando tende a pela esquerda, a função tende a . Já quando nos aproximamos de 4 pela direita, a função tende a . Então os limites laterais são diferentes e não existe.
Já o valor de pois exatamente em a bolinha está fechada e perto de .
Passo 3
Letra c): e o limite . Olhando com mais carinho pro gráfico em torno desse ponto temos:
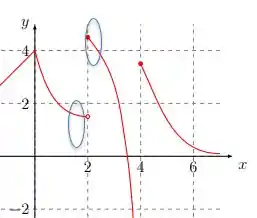
Quando tende a 2 pela esquerda temos:
E pela direita:
Como os limites são diferentes, não existe.
E a bolinha fechada acontece em .
Beleza? Vamos seguir?
Passo 4
Letra (d): e o limite . Em torno desse ponto temos:
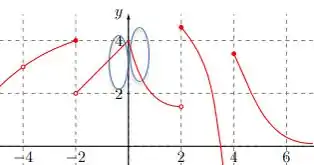
Embora seja por funções diferentes, os limites laterais tendem para um mesmo valor quando . Então esse limite existe! E vale !
E a bolinha fechada tbm está em , então .
Passo 5
Letra (e): e o limite . De novo, vamos olhar o gráfico em torno de .
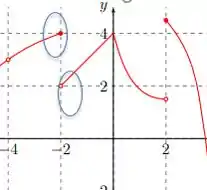
Então já vemos que os limites laterais não são iguais, então o limite nesse ponto não existe!
E a bolinha fechada? Ela está em ! Então a função vale nesse ponto.
Passo 6
Letra (f): e o limite . Agora vamos analisar a função em torno de !
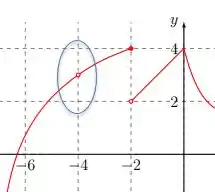
Até agora foi o ponto mais comportado! Pelos dois lados a função tende pro mesmo valor! Tanto pela esquerda, quanto pela direita a função em tende a ! Então o limite nesse ponto existe e vale:
Maaaaaasss dá uma olhada na bolinha aberta! Isso significa que a função exatamente em não está definida! E digo isso porque se tivéssemos uma reta vertical imaginária em a função não tem uma bolinha fechada em nenhum lugar! Só ali ela não está definida!
Então:
Tranquilo?
Passo 7
Letra (g):
Agora a última letra:
g) O que se pode dizer sobre a existência do limite nos pontos ?
Uma coisa: .
Então queremos saber o comportamento da função em torno de . Olhando o gráfico (pela última vez, juro!)
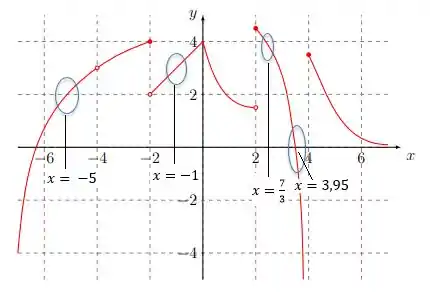
Em todos esses pontos a função é contínua! Isso significa que tanto pela direita, quanto pela esquerda, a função tende ao mesmo ponto! E no ponto a função não tem um buraquinho! Então podemos dizer que nesses pontos o limite existe!

Ufa! Terminamos!
Espero ter ajudado!
Resposta
não existe,