O gráfico de uma função está esboçado a seguir
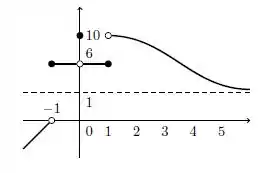
Qual das seguintes afirmações é verdadeira?
- não existe
Não é necessário justificativa.
Passo 1
Pessoal, vamos analisar esse gráfico juntos, afirmativa por afirmativa e vamos ver como é tranquilo. Começando pela letra “a”:
Essa afirmação diz que quanto mais eu aumento o , eu tendo a me aproximar do valor , vamos olhar para o gráfico:
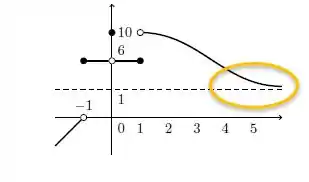
Veja que na verdade, nós estamos nos aproximando da linha que representa , então essa afirmativa está INCORRETA!
Passo 2
A letra “b” diz o seguinte:
Ou seja, essa opção afirma que quando nos aproximamos de pela esquerda e pela direita, nós encontramos o valor igual a .
Vamos começar olhando de quem se aproxima de pela esquerda, ou seja, valores menores que :
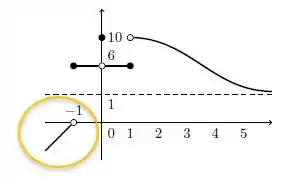
Vemos que por esse pedacinho, quanto mais nos aproximamos de , encontramos . Como isso é diferente do limite que esperávamos de :
Como o limite pela esquerda já é diferente de 6, nem precisamos calcular o limite pela direita. Mas pra você saber, quando nos aproximamos do pela direita, ou seja, pelos valores maiores que -1, chegamos perto do .
Mas não importa. Como o limite pela esquerda não é 6, já podemos dizer que a afirmativa é INCORRETA!
Passo 3
Não desanima não, vamos ver a letra “c”:
Ele só está dizendo que quando , vamos olhar no gráfico:
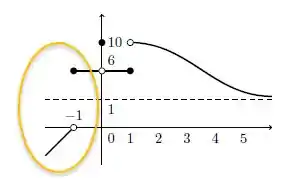
Não deixe as bolinhas te enganarem, apesar da função ir crescendo em direção a , quando vai se aproximando de , percebe que temos uma bolinha aberta (branquinha por dentro)? Isso quer dizer que a função não passa nesse ponto.
E onde temos uma bolinha fechada no ? Isso mesmo, em , ou seja:
Então essa afirmativa é INCORRETA!
Passo 4
Até agora não encontramos a nossa afirmativa verdadeira, vamos então investigar a letra “d”:
Mesma coisa que fizemos na afirmativa anterior, investigar onde a bolinha está fechada no nosso gráfico para :
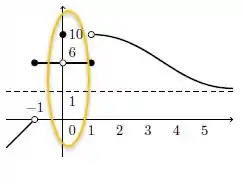
Veja que quando estamos no ponto , o gráfico está com uma bolinha aberta em e uma bolinha fechada em , isso indica que:
E essa afirmativa está INCORRETA!
Passo 5
Nossa penúltima alternativa, a letra “e” afirma:
não existe
Atenção! Para que o limite em um ponto exista, precisamos que ele seja igual pela direita e pela esquerda! Se afirmativa diz que o limite não existe, ela está dizendo que os limites são diferentes pela esquerda e pela direita. Vamos ver se isso é verdade!
Nos aproximando por valores menores que 1, ou seja, pela esquerda, encontramos valores que tendem a 6.
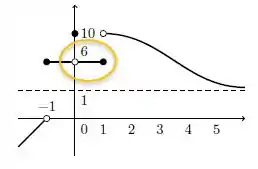
Mas perceba que se aproximamos por valores maiores que , os valores da função tendem a 10.
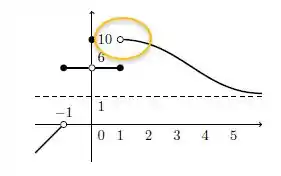
Então os limites laterais são diferentes!
Logo, o limite em realmente não existe. Essa afirmativa está CORRETA!
Resposta
Letra “e”