UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 1d.
- Defina:
- Função decrescente (num dado intervalo).
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para definir o que é uma função decrescente. Correto? E existe uma maneira bem interessante de fazermos isso, que é usando o teste de crescimento ou decrescimento de funções. Para fazermos esse teste precisaremos relembrar alguns pontos importante que estudamos em cálculo.
Vem comigo que te ajudo com isso.
Passo 2
O teste de crescimento e decrescimento de uma função é uma forma de acharmos os intervalos onde uma função é crescente e onde é decrescente. Ele é bem útil para quando precisarmos fazer o esboço do gráfico da função, por exemplo.
Ele se baseia na definição da derivada como a inclinação da reta tangente ao gráfico da função.
A derivada é uma taxa de variação, e se essa taxa for negativa temos que a função será decrescente, já que as variações mostram que o valor da frente é sempre menor que o anterior.
Podemos definir dessa maneira:
Uma função será decrescente num intervalo se:
Pra essa definição ficar mais clara, vamos da uma olhadinha no gráfico de uma função qualquer:
Passo 3
Interpretação gráfica:
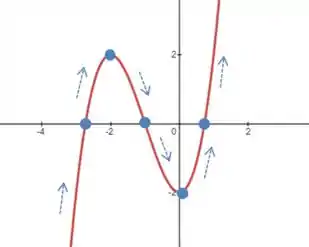
Repare que nos intervalos de a função é decrescente, e em qualquer ponto desse intervalo que nós calcularmos a derivada ela será negativa.
Sacou?! E assim definimos o que é uma função crescente dentro de um intervalo. 😊
Resposta
No desenvolvimento.