Lista 1 – 2020 – UFAM – Cálculo I – Questão 3a
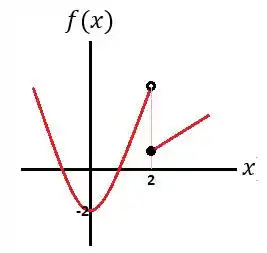
Considere a função , dada por:
Construa o gráfico de .
Passo 1
Falaeee, beleza??? Seguinte, vamos construir esse gráfico devagarinho, beleza?
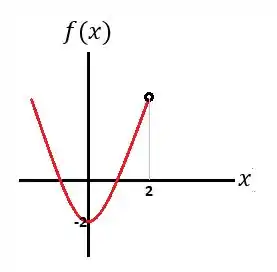
Vamos fazer primeiro :
Passo 2
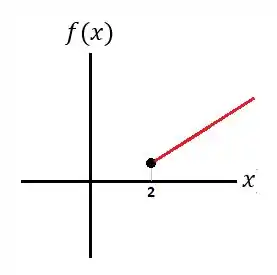
Agora, vamos fazer :
Passo 3
Agora é só juntar os dois gráficos, se liga:
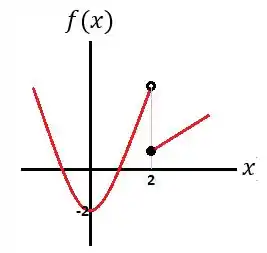
Massa né? Responde Aí!! ;)
Resposta
Exercícios de Livros Relacionados
Para o limite x 3 + x + 1 = 3 , use um gráfico para determinar o valor do δ correspondente a ε = 0,4 .Usando um sistema de computação algébrica para resolver a equação x 3 + x + 1 = 3 + ε , determine
Demonstre cada afirmação usando a definição ε , δ de limite e ilustre com um diagrama como o da Figura 9. lim x → 1 2 x + 3 = 5
Demonstre cada afirmação usando a definição ε , δ de limite. lim x → 6 x 4 + 3 = 9 2
Para o limite: lim x → 0 e x - 1 x = 1 Ilustre a Definição 2 encontrando os valores de δ que correspondam a ε = 0,5 e ε = 0,1 .
Mostre por meio de um exemplo que lim x → a ��� f x + g ( x ) ��� pode existir mesmo que nem lim x → a f ( x ) nem lim x → a g ( x ) existam.