Em , um bloco de massa está inicialmente em repouso sobre um plano horizontal e conectado a uma barra rígida de massa desprezível e comprimento que pode girar em torno do ponto O. Um torque é então aplicado à barra, tal que possui uma aceleração angular constante. Existe atrito entre e a superfície horizontal, tal que os coeficientes de atrito estático e cinético são, respectivamente e . Considere .
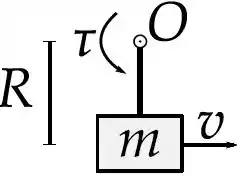
(a) Em que instante de tempo o bloco possui velocidade ?
(b) Encontre o valor do torque aplicado .
Passo 1
Primeiro de tudo...
Esse sistema está num plano horizontal. Ou seja, é como se isso estivesse girando horizontalmente em cima de uma mesa, por exemplo.
Essa seria uma imagem da gente olhando a mesa por cima:
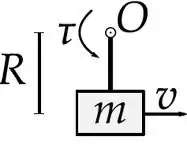
Beleza, entendemos isso.
Passo 2
Na letra (a), queremos saber em que instante nosso bloco atinge uma velocidade de .
Nós conhecemos a aceleração angular .
Então, vamos achar a velocidade angular que corresponde à velocidade linear de do bloco.
Bom, podemos relacionar a velocidade do bloco com sua velocidade angular com:
Passo 3
Agora que conhecemos a velocidade angular .
Podemos aplicar a equação de um movimento circular uniformemente acelerado, pois a aceleração angular é constante.
Para ficar fácil de lembrar, podemos fazer um paralelo com a translação...
No movimento uniformemente acelerado, temos:
Então, no movimento circular uniformemente acelerado, temos:
Substituindo os valores:
Passo 4
Já na letra (b), queremos o torque aplicado que gere essa aceleração de .
Para isso vamos utilizar a Segunda Lei de Newton para rotações:
Passo 5
E quais são os torques sobre o corpo?
Bom, temos o torque que queremos descobrir e também o torque gerado pela força de atrito que atua contra o movimento:
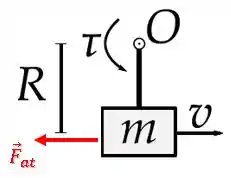
Como o bloco está deslizando, a força de atrito que atua sobre ele é uma força de atrito cinético e é calculada com:
Passo 6
Mas quanto vale essa força normal?
Olhando o bloco de frente, em vez de olhando ele por cima, temos:
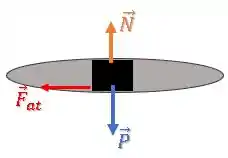
Como o bloco só se movimento no plano horizontal, ele está em equilíbrio na vertical.
Ou seja:
Substituindo isso na expressão da :
Passo 7
Agora que conhecemos a , podemos calcular o seu torque.
O torque é dado pelo produto vetorial entre o vetor e o vetor da força :
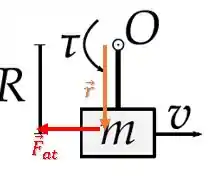
Como esses vetores são perpendiculares, o módulo do torque fica:
Passo 8
Agora, vamos voltar à Segunda Lei:
O torque está a favor do movimento enquanto o torque da força de atrito está contrário ao movimento:
Agora, só falta achar o momento de inércia desse sistema que podemos substituir os valores numéricos.
Passo 9
Como a massa da barra é desprezível, sobra apenas o bloco à uma distância do eixo de rotação.
Assim:
Passo 10
Substituindo na expressão, temos:
Aplicando os valores numéricos, temos:
Esse é o valor do torque necessário para que o bloco tenha uma aceleração angular de nessas condições.
Resposta
(a)
(b)