USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 40a
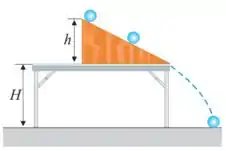
40. Uma bola de futebol, de massa e com diâmetro , rola sem deslizar sobre um plano inclinado. Ela parte do repouso e, depois de e tendo completado exatamente rotações, escapa pela borda do plano inclinado. Dado: .
(a) Calcule o torque resultante sobre a bola relativo ao seu centro de massa, enquanto ela rola sobre o plano inclinado.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos uma bola de massa e diâmetro que rola sobre um plano inclinado sem deslizar partindo do repouso e depois de e rotações completas, a bola escapa do plano e cai.
Com isso, queremos saber qual é o torque resultante na bola quando ela rola sobre o plano.
Tem ideia de como fazer isso? 😬
Sabemos que o módulo torque pode ser calculado como
Ou seja, sabemos que o momento de inercia da bola é dada por
Já pelas informações dadas no enunciado, temos que calcular a aceleração angular e substituir na fórmula.
Tranquilo? Bora lá! 😎
Passo 2
Para encontrar a aceleração angular, podemos aplicar a equação do movimento circular acelerado
A bola girou vezes antes de cair, portanto temos que
Como a bola parte do repouso, e também foi dado que a bola leva para completar o trajeto...
Substituindo essas informações na equação, temos
Isolando , vamos encontrar
E finalmente substituindo e em , vamos obter
Como e , substituindo essas informações em ...
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
