UFRJ – Física 1 2020.2 – P2 – Questão 4
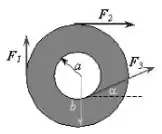
Calcule o torque resultante sobre um cilindro sob ação das forças de módulo , e em torno do centro, se e . Considere como positivo um vetor apontando para dentro da página e note que a força de módulo é tangente à circunferência interna no ponto em que a mesma intercepta a linha tracejada.
Escolha uma:
- Nenhuma das alternativas
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
O módulo do torque pode ser calculado da seguinte forma:
O símbolo se refere à distância perpendicular da linha de atuação da força até o eixo de rotação.
E o sentido? Para descobrir o sentido a gente usa a regra da mão direita. As forças e produzem um torque que aponta para dentro da página, enquanto que o torque da força aponta para fora. Sendo assim os torques associados às primeiras duas forças são positivos, enquanto que o terceiro é negativo.
Beleza até aqui?
Passo 2
O torque resultante é a soma dos torques envolvidos no corpo, então temos:
Para as distâncias temos:
As forças:
Agora é só substituir:
Analisando as alternativas, a correta é a (c).