(Capítulo 9.1 – Exercício 61) Um pêndulo consistindo em um fio de comprimento preso a uma bolinha de massa oscila em um plano vertical. Quando o fio forma um ângulo com a vertical, (a) calcule a aceleração tangencial da bolinha, usando . (b) Qual é o torque exercido em relação ao ponto pivô? (c) Mostre que , com , fornece a mesma aceleração tangencial encontrada na parte (a).
Passo 1
Oieee gente! Vamos lá falar sobre pêndulo ok?
As forças que atuam no pêndulo são as seguintes:
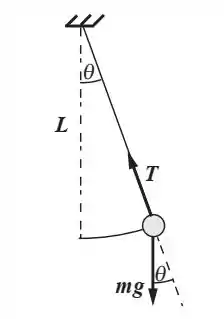
Então vamos aplicar as fórmulas que sabemos pra encontrar o que o exercício pede!!
Passo 2
a) A força tangencial que atua no pêndulo é componente do peso.
Então:
Passo 3
Passo 4
b) Como a tração da corda passa pelo ponto de aplicação, a única força que faz torque é o peso:
Então:
Passo 5
c) Da segunda lei de Newton conseguimos relacionar o torque com a aceleração angular:
O momento de inércia do pêndulo é:
Substituindo:
Mas do enunciado, , então
Que é o mesmo resultado da parte a 😊
E fimmm
Resposta
a)
b)
c) Demonstração