USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 25a
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Qual é o torque exercido sobre o cilindro?
Passo 1
Oiie, tudo bem?
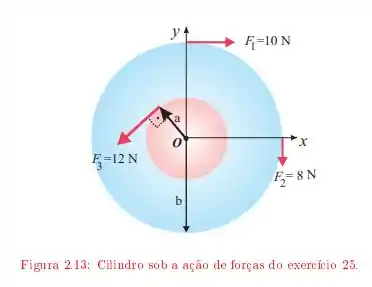
Temos um cilindro de massa , e sobre este cilindro são realizadas forças em diversas direções e posições no cilindro, como no esquema a seguir
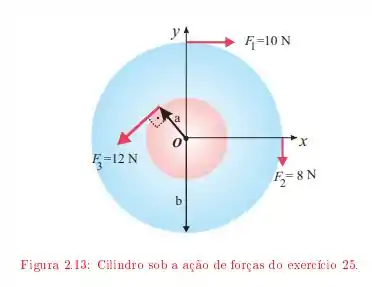
o cilindro vermelho tem raio dado por e o cilindro azul tem raio . Esta alternativa pede para que calculemos
Qual é o torque exercido sobre o cilindro?
Como podemos fazer isso? Como as forças são aplicadas tangencialmente ao cilindro, temos que o vetor posição a partir da origem é sempre perpendicular a força, de forma que
em que a o torque resultante é tal que
,
Bora Bora resolver isso!
Passo 2
O torque resultante sobre esse sistema é dado por
em módulo temos que
como esse valor é positivo, temos que a escolha do sentido horário para a rotação é a correta, sendo assim, usando a regra da mão direita podemos ver que
Essa alternativa foi isso! Te vejo na próxima! Até já!