Considere dois cilindros homogêneos, de mesma massa, porém um possui o dobro do raio do outro, conforme as figuras. Ambos os cilindros são livres para rodar em torno de um eixo que passa pelos seus respectivos centros e uma força tangencial é aplicada no topo de ambos, fazendo com que passem a girar. Para que ambos girem com a mesma aceleração angular, é preciso que:
(Dado: Se é a massa e é o raio de um cilindro homogêneo, )
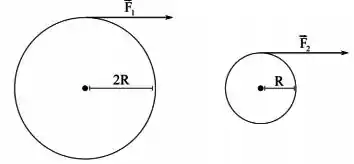
(A) A força aplicada no cilindro menor tem de ser o dobro da força aplicada no cilindro maior.
(B) A força aplicada no cilindro menor tem de ser a metade da força aplicada no cilindro maior.
(C) A força aplicada no cilindro menor tem de ser a igual à força aplicada no cilindro maior.
(D) A força aplicada no cilindro menor tem de ser 4 vezes maior que a força aplicada no cilindro maior.
(E) A força aplicada no cilindro menor tem de ser 4 vezes menor que a força aplicada no cilindro maior
Passo 1
Queremos relacionar as forças e a partir das acelerações angulares dos dois cilindros...
De que forma podemos fazer isso?
Como uma força na borda do cilindro gera um torque , uma boa forma de relacionar força com aceleração angular é a partir da segunda lei de Newton para rotações:
Se as acelerações angulares dos dois cilindros devem ser iguais, temos que:
Sabemos calcular os momentos de inércia de cada cilindro e podemos relacionar as forças e a partir dos torques que elas geram.
Passo 2
Vamos calcular os momentos de inércia...
O momento de inércia de um cilindro com relação a um eixo passando pelo seu centro de massa é dado por:
Os dois cilindros têm a mesma massa que chamaremos de .
O primeiro cilindro tem raio :
Já o cilindro 2 tem raio :
Passo 3
Agora, vamos calcular os torques de cada força.
O torque de uma força é dado pelo produto vetorial entre a posição do ponto de aplicação da força com a força em si :
Só estamos interessados no módulo do torque, que é dado por:
Como o vetor posição e o vetor força são perpendiculares em ambos os casos:
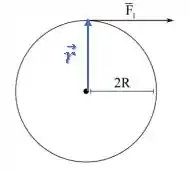
temos que o ângulo entre eles é :
Para o cilindro 1, temos:
Enquanto para o cilindro 2, temos:
Passo 4
Agora basta substituir essas expressões de torque e momento de inércia na equação inicial:
Cortando os “”s dos dois lados da equação:
Cortando “”:
Queremos a força do cilindro menor em função da outra, então:
Assim, a força no cilindro menor deve ser a metade da força no cilindro maior para que eles tenham a mesma aceleração angular.
Ficamos com a alternativa (B).
Resposta
Letra (B)