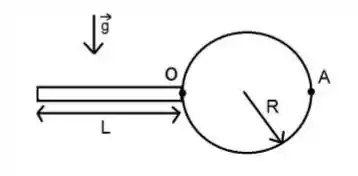
Um corpo formado por uma barra homogênea, de massa e comprimento , e por um disco, de massa e raio , pode girar em torno de um eixo que passa pelo ponto (na junção da barra e do disco) e é perpendicular ao plano da página. O corpo é mantido em repouso na horizontal, como vemos na figura. Considere .
(a) Calcule o momento de inércia da barra em relação ao eixo que passa pelo ponto . Dado: .
(b) Calcule o momento de inércia do disco em relação ao eixo que passa pelo ponto . Dado: .
(c) Calcule o módulo do torque resultante que age sobre o corpo no momento em que o corpo é solto.
(d) Calcule o módulo da aceleração adquirida pelo ponto (extremidade direita do disco) no momento em que o corpo é solto. Indique também a direção e sentido dessa aceleração.
Passo 1
(a) Pelo teorema dos eixos paralelos, temos:
Passo 2
(b) Pelo teorema dos eixos paralelos, temos:
Passo 3
(c) O torque resultante é dado pela soma dos torques devido aos pesos da barra e do disco. O peso do disco tende a girar o corpo no sentido horário e o peso da barra tende a girar o corpo no sentido anti-horário. Sendo assim, considerando que torques tendendo a girar o corpo no sentido anti-horário são positivos, temos:
Portanto, o módulo de é
Passo 4
(d) Como o torque resultante é negativo, o corpo irá girar no sentido horário, e portanto o ponto acelera para baixo quando o corpo é solto. O módulo da aceleração pode ser encontrado pela segunda lei de Newton para rotações :
Como trata-se de uma rotação, a aceleração em um dado ponto pode ser obtida pela expressão , onde é o raio do movimento. No caso do ponto , esse raio é o diâmetro do disco, e portanto:
Resposta
(a)
(b)
(c)
(d)