Torque
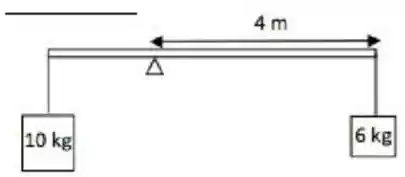
Dois corpos de massa e estão sujeitos à ação da gravidade e são pendurados por cordas na extremidade de uma barra de massa desprezível. A barra é apoiada sobre um ponto distante de uma de suas extremidades e permanece em equilíbrio, como mostrado na figura abaixo. Se a corda de apoio ao bloco é cortada encontre o torque agindo no sistema em relação ao ponto de apoio da barra.
a)
b)
c)
d)
e)
Passo 1
O peso do bloco de faz torque no sentido contrário ao torque do bloco de . Vamos utilizar isso para achar a distancia do bloco de ao eixo de rotação.
Como o sistema está em equilíbrio, o torque total é zero.
Substituindo os valores:
Após a corda ser cortada, o deixará de existir e assim ficaremos com:
Resposta
Alternativa
Exercícios de Livros Relacionados
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2