UNB – Sem Campus – Física 1 – Lista – Listas de Exercício Física 1 – UnB – Lista 12 – Dinâmica do Movimento - Questão 1 – Alternativa a)
Uma força atuando sobre uma peça de uma máquina é dada pela expressão . O vetor da origem ao ponto onde a força é aplicada é dado por .
a) Faça um diagrama mostrando , , e o sentido do torque.
Passo 1
Oiiie, tudo certinho contigo?
Temos aqui uma questão em que nos é dada uma força que atua em uma posição indicada pelo vetor em relação a origem! Este será um problema que introduzirá os conceitos de torque, assim como representa-lo, e calculá-lo. Quando estávamos no ensino médio nós calculávamos torque de uma maneira simplificada para o caso particular em que a força era perpendicular ao vetor que vinha da origem (eixo de rotação) até o ponto em que a força era aplicada. Você sabe generalizar isso para o caso de uma força em uma direção arbitrária como dada neste enunciado? Vamos dar uma olhada nisso! Belezinha?
Passo 2
A alternativa pede que façamos um esquema da força, do vetor posição, e torque realizado. Para tentarmos manter uma escala note que os componentes da força e do vetor posição, indicam o quanto desta força está em cada eixo. Por exemplo, se temos , quer dizer que temos unidades no eixo negativo e unidades no eixo positivo. Analogamente, para o vetor , em que temos unidades no eixo negativo, e unidades no eixo postivo. Mas ainda precisamos do sentido do torque! Para isso, precisamos lembrar como ele é calculado, tente relembrar! Se travar, bora comigo!
Passo 3
O torque pode ser calculado utilizando
Ou seja, o sentido do vetor torque é obtido resolvendo o produto vetorial acima. Definido como
Usando que e , temos que
Ou seja, o torque está no sentido positivo de . Vamos desenhar nosso esquema agora!
Passo 4
Colocando em um sistema cartesiano, temos o seguinte
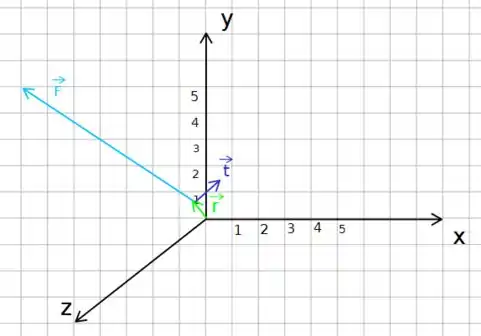
Okay! Essa é a nossa primeira alternativa! Vamos seguir para a próxima agora! Até daqui a pouco!
Resposta
Ao longo dos passos!