Um haltere é formado por duas massas idênticas , presas nas extremidades de uma haste delgada de massa desprezível e de comprimento . Esse haltere está sujeito a duas forças de mesmo módulo , sempre perpendiculares à haste que as une, apontando em sentidos opostos. As forças atuam durante um intervalo de tempo .
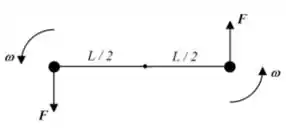
Inicialmente, o haltere está em repouso. Ao fim do intervalo de tempo , a velocidade angular do haltere será
(a)
(b)
(c)
(d)
(e)
Passo 1
Como as forças são sempre perpendiculares à haste então o torque total sobre a haste será sempre o mesmo. Cada força está a uma distância do eixo de rotação, assim
Passo 2
Como a haste tem massa desprezível o momento de inércia do haltere será somente a contribuição das duas massas , assim
Passo 3
Podemos relacionar a velocidade angular por com a aceleração angular
Queremos a velocidade angular num tempo e sabemos que inicialmente o haltere está em repouso
A aceleração angular se relaciona com o torque por meio de
Assim
Resposta
(B)