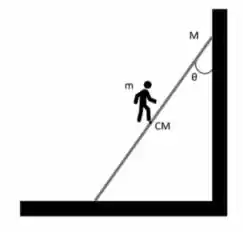
Um homem de massa sobe uma escada de massa que está no solo com coeficiente de atrito igual a , e também está apoiada na parede sem atrito formando um ângulo com a parede. Qual deve ser o ângulo limite para que o homem possa subir até o centro de massa da escada sem que ela deslize?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
A ideia aqui é equacionar tanto as forças para que o torque as resultantes sejam zero. Dá uma olhada no esquema que fiz sobre esse desenho:
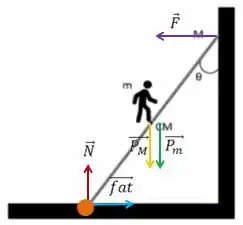
Na base da escada também estão agindo duas forças: a força normal (que é vertical para cima) por causa do contato da escada com o chão e a força de atrito que aponta no sentido oposto ao deslocamento (que não queremos) da escada.
Por fim, temos o topo da escada a força que vai apoiar a escada e nos dizer qual ângulo máximo para que não haja deslocamento da escada.
Para o eixo de rotação vou escolher o ponto de apoio da escada com o chão, representada pela bolinha em laranja no desenho.
O que queremos é equilíbrio, não é? Então precisamos que todas as somas componentes das forças e dos torques seja zero, então temos:
Como a força normal e a força de atrito atuam no eixo de rotação, elas não produzem torque.
O braço de alavanca (distância perpendicular da linha de atuação da força até o eixo de rotação) dos torques das forças peso é e o braço de alavanca da força é .
Passo 2
Da equação para o torque temos:
Daí temos:
E simplificando temos:
Tranquilo?
Passo 3
E agora da equação para a força de atrito temos que , e a força normal é o produto do coeficiente de atrito pela força normal:
E a força normal é igual a soma dos pesos do homem e da escada:
E agora vou substituir essa expressão para a força ali em cima na expressão para o ângulo :
Olha só que legal! Podemos simplificar e ficamos com uma expressão bem simples para o ângulo, saca só:
Como , então:
Assim o ângulo máximo é .
Beleza?
Espero ter te ajudado!
Pronto pra próxima questão? =)