Uma pequena esfera ligada a uma extremidade de uma haste rígida leve gira em torno de um eixo perpendicular que está fixado à outra extremidade da haste. Em um certo sistema de referências, a sua velocidade angular é negativa, e a sua aceleração angular é negativa. Observando o sistema a partir da direção positiva do eixo de rotação, a esfera está:
a) girando no sentido horário e desacelerando.
b) girando no sentido anti-horário e desacelerando.
c) girando no sentido horário e acelerando.
d) girando no sentido anti-horário e acelerando.
e) Primeiro girando no sentido anti-horário e, em seguida, no sentido horário.
Passo 1
Adotando um sistema de coordenadas, podemos representar o vetor posição da esfera e como o enunciado informou que a velocidade angular é negativa utilizamos , ou seja, a velocidade angular ficará para baixo.
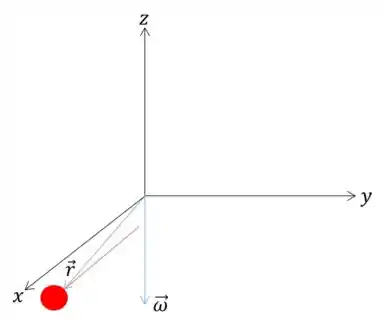
Agora para descobrir para que lado a bolinha está girando, basta utilizar a regra da mão direita na relação:
Utilizando a regra da mão direita, vemos que o vetor velocidade aponta para a esquerda.
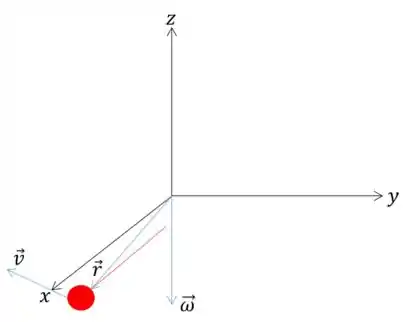
Ou seja, a bolinha está girando no sentido horário!
Além disso, tanto a velocidade angular quando a aceleração angular são negativas, ou seja, estão no mesmo sentido. Portanto o movimento é acelerado.
Resposta
Alternativa