Torque
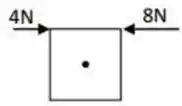
Um quadrado homogêneo de madeira de comprimento de lado é colocado sobre uma mesa horizontal e está livre para girar em torno de seu eixo central. O quadrado está sujeito a duas forças como mostrado na figura. Qual a magnitude do torque resultante sobre o quadrado em relação ao eixo de rotação?
a)
b)
c)
d)
e)
Passo 1
Muito bem, temos duas forças girando o quadrado em sentidos contrários. Pela formula:
Para as duas forças, a distância até o eixo de rotação é igual a metade da diagonal do quadrado, portanto, ficamos com:
Essas duas forças fazem um ângulo de com os vetores de posição
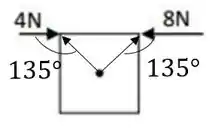
Assim, tomando como positivo o torque que faz rotações na direção anti-horária, teremos
Resposta
Alternativa .
Exercícios de Livros Relacionados
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2