Questão 1) Dois blocos pequenos de massas iguais, , estão fixos em uma gangorra sem atrito, de massa desprezível e de comprimento , distantes de e do eixo de rotação. Inicialmente a gangorra encontra-se na horizontal, em repouso. Calcule o módulo da aceleração tangencial do bloco imediatamente após a gangorra ser liberada. Forneça sua resposta apenas em termos da aceleração da gravidade g.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

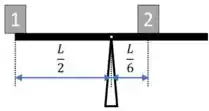
Nessa questão, temos uma gangorra, travada, de tamanho que na extremidade da esquerda há um bloco de massa que vamos chamar de Bloco .
No lado direito da gangorra temos um outro bloco de massa que está a uma distância do centro da gangorra, vamos chamar esse bloco de Bloco .
Nessa situação, assim que destravarmos a gangorra queremos descobrir qual é a aceleração tangencial do Bloco !
Tem alguma ideia do que fazer?? 🤔🤔
Que tal usarmos a ideia do torque resultante para obter a força de rotação da gangorra?
Assim podemos fazer algumas analogias entre o torque e a aceleração angular e depois com a aceleração tangencial.
Entendeu?
Bora ver na prática! 😉
Passo 2
Para obter o torque resultante podemos calcular a contribuição do torque de cada bloco para a gangorra.
Lembra como calculamos o torque de alguma coisa?
Uma das maneiras é calcular o produto entre a força, o seno do ângulo entre o vetor força e o eixo do raio de rotação e a distância da aplicação da força até o eixo de rotação, como por exemplo em

No nosso caso o ângulo entre o vetor força e raio de rotação é , ou seja, .
Logo o módulo do torque no nosso caso é dado por
Para o Bloco , qual é o raio e a força ?
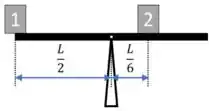
O raio é a distância da força até o eixo de rotação, ou seja, analisando a imagem e a descrição do enunciado .
Já a força é a força peso do bloco, concorda? Se a força peso é dada por , então .
Portanto
Entendeu essa parte? 😁
Fazendo a mesma análise para o Bloco , vemos que a distância até o eixo de rotação é e da mesma forma do Bloco a força que o Bloco exerce sobre a gangorra é a força peso do bloco, ou seja, .
Dessa forma o torque produzido pelo Bloco é.
Considerando o sentido anti-horário como positivo e horário como negativo, o torque resultante é dado por
Fazendo as substituições
Encontramos o torque resultante, e agora? 🤔
Passo 3
Temos uma outra maneira de calcular o torque, não é? Mas relaxa, não queremos confirmar o resultado que obtivemos no passo anterior. Nós podemos usar essa outra forma pra fazer uma relação muito interessante.
Ta lembrado que o torque também pode ser calculado como o momento de inércia multiplicado pela aceleração angular?
Mas o que é ?
O momento de inércia de um objeto pontual é dado por , não é?
E a aceleração angular ?
Podemos escrever a aceleração angular como a razão entre a aceleração tangencial com o raio de rotação, ou seja,
Calculando o momento de inércia do sistema, vamos obter
Concorda?
Interessante, né? 😉
Passo 4
Para o Bloco o momento de inércia é calculada sabendo que
Agora para o Bloco o momento de inércia é obtido sabendo que
Dessa forma, o momento resultante será
Fazendo as devidas substituições de e de em
Como estamos analisando o Bloco , o que falta é a distância do bloco até o eixo de rotação .
Simplificando a equação
Agora temos duas equações que descrevem a mesma coisa!
Está acompanhando? 👀
Passo 5
Está percebendo a maldade? Vamos igualar as equações do torque resultante que obtemos. e
Podemos simplificar a igualdade cortando dos dois lados, veja só
Isolando em um lado da igualdade, vamos obter
Simplificando...
Logo, vemos que a aceleração tangencial é dada por da aceleração gravitacional!
Muito legal, não é? 😁
É isso! Essa resolução te ajudou? Responde Aí! ✌
