Força e Leis de Newton, Dinâmica de Rotação
Seja uma barra de comprimento sobre a qual agem as forças ilustradas acima e sejam as seguintes equações:
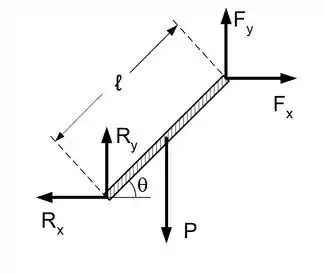
Diga quais são as equações para a situação de equilíbrio estático, tomando como origem dos torques a extremidade superior da barra.
e
e
e
e
nenhuma das respostas acima.
Passo 1
Como o corpo está em equilíbrio estático, devemos ter primeiramente o somatório das forças igual a zero, calculando separadamente as componentes e , temos:
Para :
Para :
Beleza, já descobrimos duas das equações, do movimento!
Passo 2
Agora vamos para o movimento rotacional. Como temos o corpo em equilíbrio estático, temos que o somatório dos torques também deve ser zero. Ahh...não se esqueça que devemos tomar a extremidado superior da barra como origem dos torques, então vamos lá!
Como e estão aplicadas justamente na nossa origem, elas não produzem torque!
Então vamos calcular o torque produzido por .
Veja que adotamos o sentido anti-horário como positivo!
Passo 3
Agora podemos calcular o torque produzido por e :
Show! Agora que temos todos os torques , podemos somar e igualar a zero!
Substituindo, temos:
Pronto!
Agora sim temos todas as equações! Portanto, somente as equações 1, 2 e 4 modelam esse sistema!
Resposta
e