O torque que faz uma força atuando no ponto será:
(A)
(B)
(C)
(D)
(E)
Passo 1
O torque de uma força é dado pelo produto vetorial entre e , NESSA ORDEM.
Para calcular esse produto vetorial com 3 dimensões, basta calcular o determinante dessa matriz:
Passo 2
Para calcular isso você pode fazer do jeito que você mais gostar (tem vários, mas que são a mesma coisa).
Vou sugerir um método bem de boas de calcular.
Você vai quebrar esse determinante 3x3 em três determinantes 2x2 (um para cada coordenada).
Olha só como fica... lembrando que o termo do meio tem um sinal de menos:
Passo 3
Para calcular o , tampamos a coluna e calculamos o determinante das outras duas colunas:
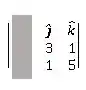
Passo 4
Para calcular o , tampamos a coluna e calculamos o determinante das outras duas colunas:
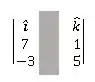
Passo 5
Para calcular o , tampamos a coluna e calculamos o determinante das outras duas colunas:
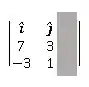
Passo 6
Então o nosso determinante 3x3 e também o nosso torque ficaram:
Ficamos com a letra (A).
Resposta
Letra (A)